Fixed and Floating Point architecture refers to the format used to store and manipulate the audio data within digital audio devices. What do these really mean you may ask, and which is superior?
‘Fixed point’ refers to the way in which a number can be represented, both before and after the decimal point, by a fixed number of digits. With floating-point representation, the placement of the decimal point can ‘float’ depending on the number being represented. This allows for greater accuracy and the ability to represent much smaller and larger values, and thereby a larger possible dynamic range in audio terms (the difference between these two values).
For example, a simple illustration of this point using 2 decimal places could be 123.45, 1234.56, 12345.67, etc, whereas a floating-point representation could, in addition represent 1.234567, 123456.7, 0.00001234567, 1234567000000000, etc. In terms of audio you can see that with floating point the level of accuracy is that much greater. The rounding and truncation of any value is unavoidable in a fixed point system. In this example you can see that the fixed point system cannot accurately represent any value more precise than 2 decimal places. Bottom line, this sounds different! This is due to quantisation error and noise caused by the variation between the true analogue value and the digital value achieved by the system in recreating the signal. This also occurs in a fixed point system when the value is recalculated, for example ‘when a gain change is applied to the digital audio on the DAW mixer or via say an EQ on a plug-in’. This is why dithering is often introduced. It’s a low level, random white noise that rounds off the value, as opposed to aggressively truncating it. The trade off here is that the fixed point system also has poorer SNR (Signal To Noise Ratio).
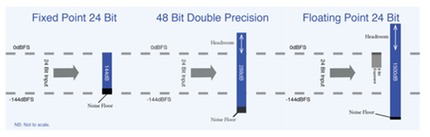
To fully understand how this relates to digital audio it’s also useful to discuss the audio bit rate resolution further, the accuracy in which analogue amplitude can be represented in the digital domain. For example, a fixed-point value at 24bit will produce 144dB of dynamic range and the representative numbers has a fixed amount of decimal places, which cannot be exceeded. As illustrated below a floating-point value of 24bit would produce over 1500dB due to an additional 8 being used as the exponent (the multiplier of the original value that defines the scale) otherwise known in this instance as 32 bit Floating Point. This far increased dynamic range gives you the ability to rescue clipped audio files because headroom is now pretty much limitless. 0dBfs still applies in a monitoring situation, as you have to consider that your D/A will be integer and will therefore clip if you exceed full range, It’s also worth noting that D/A converters recreate a representation of the waveforms they are playing back which can result in slightly different interpretations of the amplitude. Of course correct gain structure eradicates this becoming a problem in either number system. The 144dB of dynamic range a 24bit fixed system offers is ample and allows us to capture sound that is both too low in level for us to hear and that is too loud for us to bear. It’s therefore only improvements to resolution and distortions that should factor.
Some manufacturers also still use fixed point in their DSP technology, often employing ‘double precision’ which basically means 48-bit is used for internal processing, reducing the truncation issues found at the lower bit rates but without the extensive dynamic range and exceptional signal to noise ration of a full floating point system (see diagram).
With the latest Pro Tools HD, perhaps one of the last DAW’s to adopt floating point now moving over and 32 bit converters slowly entering the market, the argument is now becoming more redundant as the choice is being made for you but certainly, if you have an older system, this in itself could have more of an impact to your audio if upgrading than almost anything else!